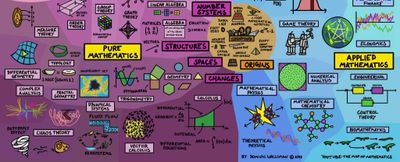
Pure Mathematics
Broadly speaking, pure mathematics is mathematics that studies entirely abstract concepts.
One central concept in pure mathematics is the idea of generality; pure mathematics often exhibits a trend towards increased generality. Uses and advantages of generality include the following:
- Generalizing theorems or mathematical structures can lead to deeper understanding of the original theorems or structures
- Generality can simplify the presentation of material, resulting in shorter proofs or arguments that are easier to follow.
- One can use generality to avoid duplication of effort, proving a general result instead of having to prove separate cases independently, or using results from other areas of mathematics.
- Generality can facilitate connections between different branches of mathematics. Category theory is one area of mathematics dedicated to exploring this commonality of structure as it plays out in some areas of math.
Pure mathematics is comprised of 4 major sub-branches:
- Quantitative Mathematics starts with numbers, first the familiar natural numbers and integers ("whole numbers") and arithmetical operations on them, which are characterized in arithmetic.
- Structural Mathematics (Abstract Algebra) deals with many mathematical objects, such as sets of numbers and functions which exhibit internal structure as a consequence of operations or relations that are defined on the set.
- Spatial Mathematics starts with the study of space originating with geometry – in particular, Euclidean geometry, which combines space and numbers,
- Mathematical Analysis (Change Mathematics) is the branch of mathematics dealing with limits and related theories, such as differentiation, integration, measure, infinite series, and analytic functions.
1. Quantitative Mathematics
Quantitative Mathematics starts with the quantity of numbers, first the familiar natural numbers and integers ("whole numbers") and arithmetical operations on them, which are characterized in arithmetic. The deeper properties of integers are studied in number theory, from which come such popular results as Fermat's Last Theorem. The twin prime conjecture and Goldbach's conjecture are two unsolved problems in number theory. As the number system is further developed, the integers are recognized as a subset of the rational numbers ("fractions"). These, in turn, are contained within the real numbers, which are used to represent continuous quantities. Real numbers are generalized to complex numbers. These are the first steps of a hierarchy of numbers that goes on to include quaternions and octonions. Consideration of the natural numbers also leads to the transfinite numbers, which formalize the concept of "infinity". According to the fundamental theorem of algebra all solutions of equations in one unknown with complex coefficients are complex numbers, regardless of degree. Another area of study is the size of sets, which is described with the cardinal numbers. These include the aleph numbers, which allow meaningful comparison of the size of infinitely large sets.
- Natural Numbers
In mathematics, the natural numbers are those used for counting (as in "there are six coins on the table") and ordering (as in "this is the third largest city in the country"). In common language, words used for counting are "cardinal numbers" and words used for ordering are "ordinal numbers". The natural numbers are the basis from which many other number sets may be built by extension: the integers, by including (if not yet in) the neutral element 0 and an additive inverse (−n) for each nonzero natural number n; the rational numbers, by including a multiplicative inverse (1/n) for each nonzero integer n (and also the product of these inverses by integers); the real numbers by including with the rationals the limits of (converging) Cauchy sequencesof rationals; the complex numbers, by including with the real numbers the unresolved square root of minus one (and also the sums and products thereof); and so on. These chains of extensions make the natural numbers canonically embedded (identified) in the other number systems. Properties of the natural numbers, such as divisibility and the distribution of prime numbers, are studied in number theory. Problems concerning counting and ordering, such as partitioning and enumerations, are studied in combinatorics. - Integers
An integer (from the Latin integer meaning "whole") is a number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, 5 1⁄2, and √2 are not. Z is a subset of the set of all rational numbers Q, in turn a subset of the real numbers R. Like the natural numbers, Z is countably infinite. The integers form the smallest group and the smallest ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers to distinguish them from the more general algebraic integers. In fact, the (rational) integers are the algebraic integers that are also rational numbers. - Rational Numbers
In mathematics, a rational number is any number that can be expressed as the quotient or fraction p/q of two integers, a numerator p and a non-zero denominator q. Since q may be equal to 1, every integer is a rational number. The set of all rational numbers, often referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by a boldface Q (or blackboard bold). - Real Numbers
In mathematics, a real number is a value of a continuous quantity that can represent a distance along a line. The adjective real in this context was introduced in the 17th century by René Descartes, who distinguished between real and imaginary roots of polynomials. The real numbers include all the rational numbers, such as the integer −5 and the fraction 4/3, and all the irrational numbers, such as √2 (1.41421356..., the square root of 2, an irrational algebraic number). Included within the irrationals are the transcendental numbers, such as π (3.14159265...). In addition to measuring distance, real numbers can be used to measure quantities such as time, mass, energy, velocity, and many more. Real numbers can be thought of as points on an infinitely long line called the number line or real line, where the points corresponding to integers are equally spaced. - Complex Numbers
A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers, and i is a solution of the equation x2 = −1. Because no real number satisfies this equation, i is called an imaginary number. For the complex number a + bi, a is called the real part, and b is called the imaginary part. Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers, and are fundamental in many aspects of the scientific description of the natural world. The complex number system can be defined as the algebraic extension of the ordinary real numbers by an imaginary number i. This means that complex numbers can be added, subtracted, and multiplied, as polynomials in the variable i, with the rule i2 = −1 imposed. Furthermore, complex numbers can also be divided by nonzero complex numbers. Overall, the complex number system is a field.
2. Structural Mathematics ( Abstract Algebra )
In structural mathematics (Abstract Algebra), many mathematical objects, such as sets of numbers and functions, exhibit internal structure as a consequence of operations or relations that are defined on the set. Mathematics then studies properties of those sets that can be expressed in terms of that structure; for instance number theory studies properties of the set of integers that can be expressed in terms of arithmetic operations. Moreover, it frequently happens that different such structured sets (or structures) exhibit similar properties, which makes it possible, by a further step of abstraction, to state axioms for a class of structures, and then study at once the whole class of structures satisfying these axioms. Thus one can study groups, rings, fields and other abstract systems; together such studies (for structures defined by algebraic operations) constitute the domain of abstract algebra. By its great generality, abstract algebra can often be applied to seemingly unrelated problems; for instance a number of ancient problems concerning compass and straightedge constructions were finally solved using Galois theory, which involves field theory and group theory. Another example of an algebraic theory is linear algebra, which is the general study of vector spaces, whose elements called vectors have both quantity and direction, and can be used to model (relations between) points in space. This is one example of the phenomenon that the originally unrelated areas of geometry and algebra have very strong interactions in modern mathematics. Combinatorics studies ways of enumerating the number of objects that fit a given structure. Some areas of mathematics that fall under the classification abstract algebra have the word algebra in their name; linear algebra is one example. Others do not: group theory, ring theory, and field theory are examples.
- Combinatorics
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics, from evolutionary biology to computer science, etc. Subfields are:- Enumerative combinatorics
- Analytic combinatorics
- Analytic combinatorics
- Partition theory
- Graph theory
- Design theory
- Finite geometry
- Order theory
- Matroid theory
- Extremal combinatorics
- Probabilistic combinatorics
- Algebraic combinatorics
- Combinatorics on words
- Geometric combinatorics
- Topological combinatorics
- Arithmetic combinatorics
- Infinitary combinatorics
- Number Theory
Number theory, or in older usage arithmetic, is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well as the properties of objects made out of integers (e.g., rational numbers) or defined as generalizations of the integers (e.g., algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of analytical objects (e.g., the Riemann zeta function) that encode properties of the integers, primes or other number-theoretic objects in some fashion (analytic number theory). One may also study real numbers in relation to rational numbers, e.g., as approximated by the latter (Diophantine approximation). The older term for number theory is arithmetic. - Group Theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces, can all be seen as groups endowed with additional operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right. Various physical systems, such as crystals and the hydrogen atom, may be modelled by symmetry groups. Thus group theory and the closely related representation theory have many important applications in physics, chemistry, and materials science. Group theory is also central to public key cryptography. - Graph Theory
In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices, nodes, or points that are connected by edges, arcs, or lines. Graphs can be directed or undirected. Graphs are one of the prime objects of study in discrete mathematics. - Order Theory
Order theory is a branch of mathematics which investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary. - Elementary algebra
The part of algebra that is usually taught in elementary courses of mathematics. - Abstract algebra
In which algebraic structures such as groups, rings and fields are axiomatically defined and investigated. - Linear algebra
In which the specific properties of linear equations, vector spaces and matrices are studied. Algebraic structures, with their associated homomorphisms, form mathematical categories. Category theory is a formalism that allows a unified way for expressing properties and constructions that are similar for various structures. - Universal Algebra
Universal algebra (sometimes called general algebra) is the field of mathematics that studies algebraic structures themselves, not examples ("models") of algebraic structures. For instance, rather than take particular groups as the object of study, in universal algebra one takes the class of groups as an object of study. - Boolean algebra
A branch of algebra abstracting the computation with the truth values false and true. - Commutative algebra
Commutative algebra is the branch of algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra. Prominent examples of commutative rings include polynomial rings, rings of algebraic integers, including the ordinary integers, and p-adic integers. - Computer algebra
The implementation of algebraic methods as algorithms and computer programs. - Homological algebra
The study of algebraic structures that are fundamental to study topological spaces. - Algebraic number theory
In which the properties of numbers are studied from an algebraic point of view. - Algebraic geometry
A branch of geometry, in its primitive form specifying curves and surfaces as solutions of polynomial equations. - Algebraic combinatorics
In which algebraic methods are used to study combinatorial questions. - Relational algebra
A set of finitary relations that is closed under certain operators. - Algebra over a field or more generally algebra over a ring.
Many classes of algebras over a field or over a ring have a specific name: - Algebra In measure theory
- Algebra In category theory
- Algebra In logic
3. Spatial Mathematics
In spatial Mathematics the study of space originates with geometry – in particular, Euclidean geometry, which combines space and numbers, and encompasses the well-known Pythagorean theorem.
- Geometry
Geometry (from the Ancient Greek: γεωμετρία; geo- "earth", -metron "measurement") is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer. - Trignonometry
Trigonometry (from Greek trigōnon, "triangle" and metron, "measure"[1]) is a branch of mathematics that studies relationships involving lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. - Differential Geometry
Differential geometry is a mathematical discipline that uses the techniques of differential calculus, integral calculus, linear algebraand multilinear algebra to study problems in geometry. The theory of plane and space curves and surfaces in the three-dimensional Euclidean space formed the basis for development of differential geometry during the 18th century and the 19th century. - Topology
In mathematics, topology (from the Greek τόπος, place, and λόγος, study) is concerned with the properties of space that are preserved under continuous deformations, such as stretching, crumpling and bending, but not tearing or gluing. This can be studied by considering a collection of subsets, called open sets, that satisfy certain properties, turning the given set into what is known as a topological space. Important topological properties include connectedness and compactness. - Fractal Geometry
In mathematics, a fractal is an abstract object used to describe and simulate naturally occurring objects. Artificially created fractals commonly exhibit similar patterns at increasingly small scales. It is also known as expanding symmetry or evolving symmetry. If the replication is exactly the same at every scale, it is called a self-similar pattern. An example of this is the Menger sponge. Fractals can also be nearly the same at different levels. This latter pattern is illustrated in small magnifications of the Mandelbrot set. Fractals also include the idea of a detailed pattern that repeats itself. - Measure Theory
In mathematical analysis, a measure on a set is a systematic way to assign a number to each suitable subset of that set, intuitively interpreted as its size. In this sense, a measure is a generalization of the concepts of length, area, and volume. A particularly important example is the Lebesgue measure on a Euclidean space, which assigns the conventional length, area, and volume of Euclidean geometry to suitable subsets of the n-dimensional Euclidean space Rn. For instance, the Lebesgue measure of the interval[0, 1] in the real numbers is its length in the everyday sense of the word – specifically, 1.
4. Change Mathematics (Analysis)
In change mathematics, understanding and describing change is a common theme in the natural sciences, and calculus was developed as a powerful tool to investigate it. Functions arise here, as a central concept describing a changing quantity. Mathematical analysis is the branch of mathematics dealing with limits and related theories, such as differentiation, integration, measure, infinite series, and analytic functions. These theories are usually studied in the context of real and complex numbers and functions. Analysis evolved from calculus, which involves the elementary concepts and techniques of analysis. Analysis may be distinguished from geometry; however, it can be applied to any space of mathematical objects that has a definition of nearness (a topological space) or specific distances between objects (a metric space).
- Calculus
It has two major branches, differential calculus (concerning rates of change and slopes of curves), and integral calculus (concerning accumulation of quantities and the areas under and between curves). These two branches are related to each other by the fundamental theorem of calculus. Both branches make use of the fundamental notions of convergence of infinite sequences and infinite series to a well-defined limit - Vector Calculus
Vector calculus, or vector analysis, is a branch of mathematics concerned with differentiation and integration of vector fields, primarily in 3-dimensional Euclidean space The term "vector calculus" is sometimes used as a synonym for the broader subject of multivariable calculus, which includes vector calculus as well as partial differentiation and multiple integration. Vector calculus plays an important role in differential geometry and in the study of partial differential equations. Vector calculus studies various differential operators defined on scalar or vector fields, which are typically expressed in terms of the del operator, also known as "nabla". Del is used to calculate the gradient, curl, divergence, and Laplacian of various object like Scalar fields, Vector fields and Vectors and pseudovectors - Differential Equations
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders. Differential equations play a prominent role in engineering, physics, economics, biology, and other disciplines. - Dynamical Systems
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a lake. At any given time, a dynamical system has a state given by a tuple of real numbers (a vector) that can be represented by a point in an appropriate state space (a geometrical manifold). The evolution rule of the dynamical system is a function that describes what future states follow from the current state. Often the function is deterministic, that is, for a given time interval only one future state follows from the current state. However, some systems are stochastic, in that random events also affect the evolution of the state variables. - Real analysis
Real analysis (traditionally, the theory of functions of a real variable) is a branch of mathematical analysis dealing with the real numbers and real-valued functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real numbers, and continuity, smoothness and related properties of real-valued functions. - Complex Analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including algebraic geometry, number theory, analytic combinatorics, applied mathematics; as well as in physics, including the branches of hydrodynamics, thermodynamics, and particularly quantum mechanics. By extension, use of complex analysis also has applications in engineering fields such as nuclear, aerospace, mechanical and electrical engineering. - Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure (e.g. inner product, norm, topology, etc.) and the linear operators acting upon these spaces and respecting these structures in a suitable sense. The historical roots of functional analysis lie in the study of spaces of functions and the formulation of properties of transformations of functions such as the Fourier transform as transformations defining continuous, unitary etc. operators between function spaces. This point of view turned out to be particularly useful for the study of differential and integral equations. - Measure theory
A measure on a set is a systematic way to assign a number to each suitable subset of that set, intuitively interpreted as its size. In this sense, a measure is a generalization of the concepts of length, area, and volume. A particularly important example is the Lebesgue measure on a Euclidean space, which assigns the conventional length, area, and volume of Euclidean geometry to suitable subsets of the {\displaystyle n-dimensional Euclidean space. For instance, the Lebesgue measure of the interval [0,1] in the real numbers is its length in the everyday sense of the word – specifically, 1. - Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to general symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). - Chaos Theory
Chaos theory is a branch of mathematics focusing on the behavior of dynamical systems that are highly sensitive to initial conditions. 'Chaos' is an interdisciplinary theory stating that within the apparent randomness of chaotic complex systems, there are underlying patterns, constant feedback loops, repetition, self-similarity, fractals, self-organization, and reliance on programming at the initial point known as sensitive dependence on initial conditions. The butterfly effect describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state, e.g. a butterfly flapping its wings in China can cause a hurricane in Texas. Small differences in initial conditions, such as those due to rounding errors in numerical computation, yield widely diverging outcomes for such dynamical systems, rendering long-term prediction of their behavior impossible in general. This happens even though these systems are deterministic, meaning that their future behavior is fully determined by their initial conditions, with no random elements involved. In other words, the deterministic nature of these systems does not make them predictable. This behavior is known as deterministic chaos, or simply chaos.
Copyright © 2024 Sanjeev Katariya - All Rights Reserved.
Powered by GoDaddy